| |
Click here for full text:
On the number of t-ary trees with a given path length
Seroussi, Gadiel
HPL-2004-127
Keyword(s): binary trees; t-ary trees; path length; universal types
Abstract: Please note: This abstract contains mathematical formula which cannot be represented here. We show that the number of t-ary trees with path length equal to p is 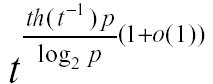 where h(x)=-xlog2x-(1-x)log2(1-x) is the binary entropy function. Besides its intrinsic combinatorial interest, the question recently arose in the context of information theory, where the number of t-ary trees with path length p estimates the number of universal types, or, equivalently, the number of different possible Lempel-Ziv'78 dictionaries for sequences of length p over an alphabet of size t. "Some of the most instructive applications of the mathematical theory of trees to the analysis of algorithms are connected with formulas for counting how many different trees there are of various kinds." D. E. Knuth, [7, p. 386].
10 Pages
Back to Index
|
Printable version
