Click here for full text:
The Empirical Distribution of Rate-Constrained Source Codes
Weissman, Tsachy; Ordentlich, Erik
HPL-2003-253
Keyword(s): rate-distortion theory; sample converse; denoising; empirical distribution
Abstract:Please Note. This abstract contains mathematical formulae
which cannot be represented here. Let X = (X1, ...) be a stationary
ergodic finite-alphabet source, Xn denote its first
n symbols, and Yn be the codeword assigned to Xn
by a lossy source code. The empirical kth-order joint distribution
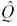 k[Xn,
Yn](xk, yk) is defined as the frequency
of appearances of pairs of k-strings (xk, yk) along
the pair (Xn, Yn). Our main interest is in the sample
behavior of this (random) distribution. Letting I(Qk) denote
the mutual information I( Xk; Yk ) when (Xk,
Yk) ˜ Qk we show that for any
(sequence of) lossy source code(s) of rate ≤ R
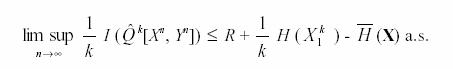
where 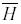 (X)
denotes the entropy rate of X. This is shown to imply, for a large
class of sources including all i.i.d. sources and all sources satisfying
the Shannon lower bound with equality, that for any sequence of codes
which is good in the sense of asymptotically attaining a point
on the rate distortion curve
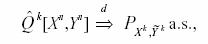
whenever PXkYk is the unique distribution attaining the
minimum in the definition of the kth-order rate distortion function. Further
consequences of these results are explored. These include a simple proof
of Kieffer's sample converse to lossy source coding, as well as pointwise
performance bounds for compression-based denoisers. Notes:
27 Pages
Back to Index
| 
printable version
